

Does increasing the number of air molecules decrease the speed of sound? If so, how? Do more particles make it more difficult for energy to travel? If so, why? I suppose the mass of the air correspond with the number of air molecules as well as what the air is made up with.
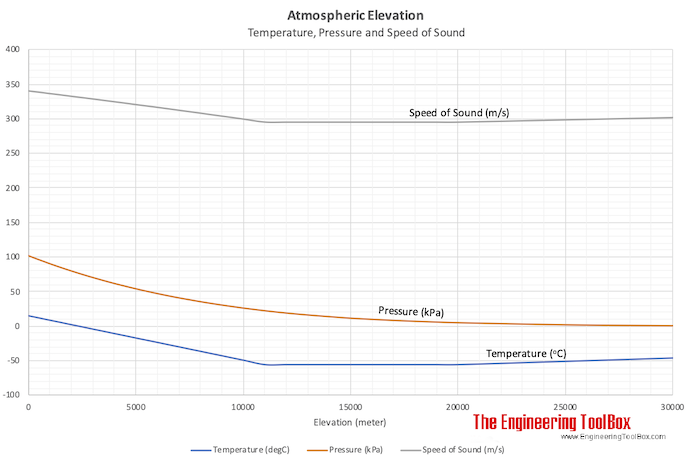
So how could mass of the air affect sound's velocity as it passes through? I don't know. of the International Standard Atmosphere values for ambient temperature, pressure, density, and speed of sound for the input geopotential altitude. Mars also has an atmosphere composed of mostly carbon dioxide. Scientists and engineers have created a mathematical model of the atmosphere to help them account for the changing effects of temperature with altitude. On Earth, the atmosphere is composed of mostly diatomic nitrogen and oxygen, and the temperature depends on the altitude in a rather complex way. With lower temperatures the movement of the gas molecules will slow down, making it more difficult for sound to travel through this medium (I am aware that I might be too general in my explanation).īut a formula I came across - # c_s = \sqrt (\frac) # - where # \gamma # is the adiabatic exponent, # k # Boltzmann's constant, # T # the temperature, and # m # the mass, seems to indicate to me that there is another variable, # m # to consider. The speed of sound varies from planet to planet. If we consider the atmosphere on a standard day at sea level static conditions, the speed of sound is about 761 mph, or 1100 feet/second. Air pressure by itself does not change the speed of sound, however temperature does and since its colder at high altitude than at sea level, the speed of sound. Although the most extreme effects of dispersion are masked by simultaneously increased attenuation, decreases in traveltime of several percent are predicted at frequencies slightly below 1 Hz, demonstrating that this dispersion must be taken into account in order to correctly predict atmospheric returns at low frequencies.This is what I am pondering about: At high altitudes, it makes sense tha t lower temperatures will correspond with velocity of sound travelling through the air at higher altitudes. c ( x R x T / M) c the speed of sound in an ideal gas R the molar gas constant (set at approximately 8.313,5 J) Adiabatic index (1.4 for air) T absolute temperature M the gas molar mass (dry air is. As the increase in altitude temperature of the air decreases, the sounds speed also. This relaxation and resulting dispersion cause sound speeds at fixed frequencies to increase significantly with altitude, and to lower the altitude at which sound is refracted downward. If you want to know the speed of sound in a gas such as air, use this unique formula. With the decrease in temperature, the speed of sound decreases.
#Speed of sound at altitude free#
Aps Q q qc ) Speed of Sound in Free Stream Speed of Sound at Sea Level Specific Heat. As altitude increases, f/ P and the mean free path increase, relaxation frequencies drop significantly, and velocity dispersion due to rotational and translational relaxation intensifies. This chapter discusses the requirement of the speed, pressure and. Since the temperature and density of air decreases with altitude, so does the speed of sound, hence a given true velocity results in a higher MACH number at. Appendix C gives the speed of sound in seawater. Special Topics Appendix B gives the variation of the speed of sound in the atmosphere with altitude. Equation (20) is the same as equation (4.3) in Reference 1. The sound travels faster through media with higher elasticity and/or lower. This speed is the phase speed of transverse traveling waves. K Bulk Modulus of Elasticity (Pa, psi) density (kg/m3, lb/ft3) This equation is valid for liquids, solids and gases. The acoustic velocity can alternatively be expressed with Hook's Law as. In the lower atmosphere, variations in the speed of sound with altitude are dominated by temperature and wind speed changes the vibrational and rotational relaxation frequencies, which depend on the ratio of frequency to pressure ( f/ P), are in the kilohertz to megahertz range. Speed of Sound in Gases, Fluids and Solids. That theory is explored in more detail to describe dispersion in the thermosphere. Dispersion is included in their treatment though emphasis is placed on absorption. Sutherland and Bass (2004) have developed a calculation of the speed of sound and attenuation at altitudes up to 160 km.


 0 kommentar(er)
0 kommentar(er)
